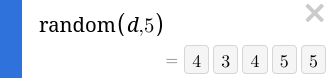4  Distributions in R and Desmos

The general operations we want to perform with distributions are

1. Compute the probability/density at specific value of \(x\)
2. Compute the probability of an interval, e.g. \(X \ge x\), \(a \le X \le b\), etc.
3. Sample random numbers from that distribution

The main distributions we will use are the binomial and normal distribution.

Note

A binomial distribution \(\operatorname{Bin}(n, p)\) is the model for: - flipping \(n\) coins where the probability of a heads is \(p\) - a multiple choice test where the probability of getting a question right is \(p\)

The probabilities for a binomial distribution is given by \[P(x\text{ successes}) = P(X = x) = {}_nC_x \cdot p^x \cdot q^{n - x}.\] We also write \(P(X = x \mid n, p)\) if we want to clarify what \(n\) and \(p\) are.

Example 4.1 For a multiple choice test where we have a \(75\%\) chance of getting a correct answer, the probability of getting \(8\) out of \(n = 10\) questions right is \[P(X = 8 \mid n = 10, p = 0.75) = {}_{10}C_8 \cdot 0.75^8 \cdot 0.25^2\] Where \[\begin{align*} {}_{10}C_8 = \frac{{}_{10}P_8}{8!} &= \frac{10 \cdot 9 \cdots (\text{eight terms})}{8!} \\ &= \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3}{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ &= \frac{10 \cdot 9}{2} = 45. \end{align*}\]

4.1 Desmos

To define a binomial distribution in Desmos, we can either use the + menu > inference > probability distribution. Or we can type out “binomialdist(n, p)” with our values for \(n\) and \(p\).

The Plus Menu in Desmos

Tip

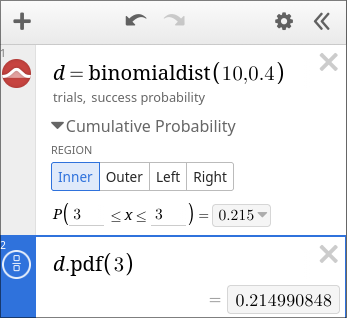
To make it possible to refer to the distribution later, I like to write “d = binomialdist(n, p)”. Then we can write things like “mean(d)” for the mean/expected value of the distribution.

4.1.1 Specific values in Desmos

We have two options.

1. We can use the \(d.\operatorname{pdf}(x)\) function.
2. We can use the Cumulative Probability menu to compute \(P(x \le X \le x)\).

E.g. for \(x = 3\):

Computing \(P(X = 3)\) in Desmos

4.1.2 Interval probabilities in Desmos

We can use the Cumulative Probability menu to compute various probabilities:

• \(P(a \le X \le b)\): Inner
• \(P(X \le a)\) or \(P(X \ge b)\): Outer
• \(P(X \le a)\): Left
• \(P(X \ge b)\): Right

4.1.3 Random numbers in Desmos

Having defined “d = binomialdist(n, p)” we can generate random numbers with this distribution using “random(d)” or if we want multiple, we can add a number like “random(d, 5).”

Random numbers in Desmos

4.1.4 Practice

1. Use Desmos to compute the probability of getting \(5\) questions right in a quiz with \(7\) questions and a probability of success \(p = 0.85\).

2. With \(X \sim \operatorname{Bin}(10, 0.7)\) compute The probability of getting between \(2\) and \(8\) successes: \(P(2 \le X \le 8)\)

3. The probability of getting at least \(5\) successes: \(P(X \ge 5)\).

4. The probability of getting less than \(5\) successes: \(P(X < 5)\).

 🎁

4.2 R

In R the functions are:

• dbinom(x, n, p) for \(P(X = x \mid n, p)\)
• pbinom(x, n, p) for \(P(X \le x \mid n, p)\)
• rbinom(k, n, p) to generate \(k\) random numbers

4.2.1 Specific values

E.g. to compute the probability of getting exactly \(5\) questions right out of \(7\) with \(p = 0.85\):

4.2.2 Intervals in R

In R the function for a left interval is pbinom(x, n, p) for \(P(X \le x \mid n, p)\). For other intervals, we might need to do some arithmetic. Such as:

\[ P(a \le X \le B) = P(X \le b \text{ and } X \not < a) = P(X \le b) - P(X \le a - 1) \] The \(a - 1\) is because \(X < a\) is the same as \(X \le a - 1\).

E.g. if \(X \sim \operatorname{Bin}(10, 0.7)\) then

1. \(P(2 \le X \le 8) = P(X \le 8) - P(X \le 1)\):

2. \(P(x \ge 5) = 1 - P(X \le 4)\):

3. \(P(X < 5) = P(X \le 4)\):

4.2.3 Random numbers in R

E.g. if we want to simulate taking a 10 question multiple choice test (with \(p = 0.7\)), 100 times, we can use rbinom(100, 10, 0.7):