2 Inclusion/Exclusion

2.1 For two sets

Example 2.1 Suppose there are $100$ CS students an a school. Of these, $50$ know Java and $60$ know Python (everyone knows at least one of these two languages). If we add $50 + 60$ we get the $100$ total students plus $10$ students who know both.

\[ 50 + 60 = 100 + 10. \]

Given two sets $A$ and $B$, we can compute $|A \cup B|$ by first adding everything in $A$ and adding everything in $B$. This counts all of $A \cup B$ except the items in $A \cap B$ were counted twice. Thus

\[ |A| + |B| = |A \cup B| + |A \cap B|. \]

2.2 For three sets

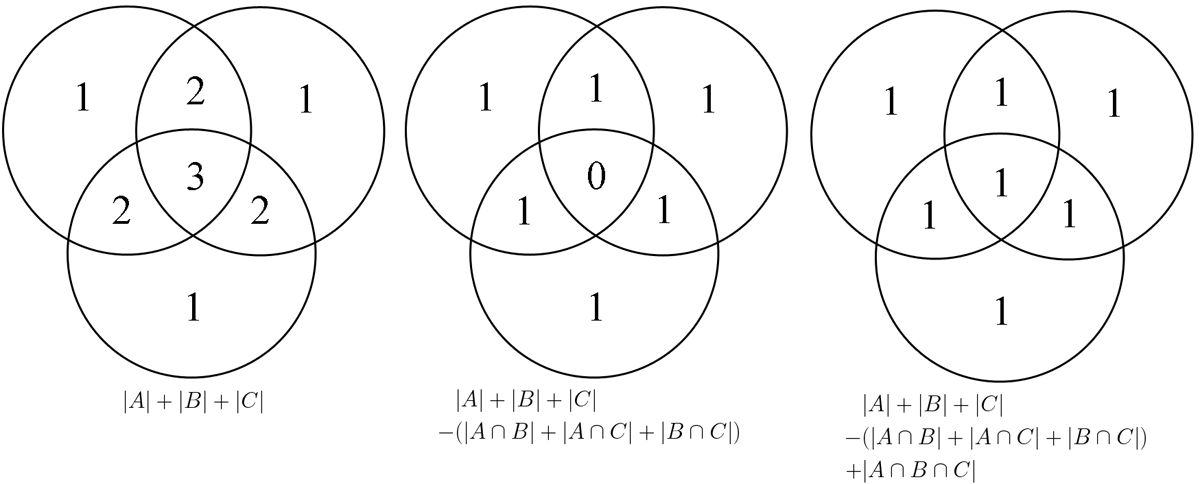
We can do a similar process for three sets. Start by adding up $|A| + |B| + |C|$ then subtract all the intersections of pairs then add back in $|A \cap B \cap C|$. For items in each region of the Venn diagram, think about how many times an item is added/subtracted overall.

E.g. items in $A$ and $B$ but not $C$ will be added in twice in the first step ($|A| + |B|$) and subtracted once in the second step ($|A \cap B|$) so they are counted once.

Items in $A \cap B \cap C$ are added in $3 - 3 + 1 = 1$ times.

2.3 Binomial coefficients and I/E

Suppose we are looking at a union of $n$ sets: $A_1 \cup \dots \cup A_n$. Consider an element $x$ belonging exactly to $A_1, \dots, A_m$ and no other sets. If we do the same procedure of adding $|A_1| + \dots + |A_n|$ then we are counting $x$ a total of $m$ times. Then, when we subtract all the pairwise intersections, $|A_i \cap A_j|$, we are subtracting from the count of $x$ a total of $\binom{m}{2}$ because there are $\binom{m}{2}$ ways to choose two indices $\{i, j\} \subset \{1, \dots, m\}$.

Thus, if we alternate: adding in single sets, subtracting pairs of intersections, adding triples, subtracting quadruples, etc. we are counting $x$ a total of

\[ \binom{m}1 - \binom{m}2 + \binom{m}3 - \binom{m}4 + \cdots \tag{2.1}\] times.

Let’s have a closer look at this. We know the Binomial Theorem says that \[ (1 + x)^m = \binom{m}0x^0 + \binom{m}1x^1 + \binom{m}2x^2 + \dots + \binom{m}mx^m. \] Substituting $x = -1$, we get

\[ 0 = \binom{m}0 - \binom{m}1 + \binom{m}2 - \dots + \binom{m}m (-1)^m. \]

And since $\binom{m}0 = 1$, if we move all the other terms to the other side of the equation, we see that Equation 2.1 evaluates to $1$.

Note 2.1

For this problem we are counting the size of $A_1 \cup \dots \cup A_n$ so each element is in at least one set ($m \ge 1$). This is important so that we can say that $0^m = 0$. In the context of the binomial theorem, $(1 - 1)^0 = \binom{0}{0} = 1$. This will be important later when we want to count elements not belonging to any set.

The general I/E formula is then

\[\begin{align*} |A_1 \cup \dots \cup A_n| &= \sum_i |A_i| - \sum_{i < j} |A_i \cap A_j| + \sum_{i < j < k} |A_i \cap A_j \cap A_k| - \dots \\ &= \sum_{t = 1}^n (-1)^{t + 1} \sum_{i_1 < \dots < i_t} |A_{i_1} \cap \dots \cap A_{i_t}|. \end{align*}\]

Note: $(-1)^{t + 1}$ takes the values $1, -1, 1, -1, \dots$ starting at $t = 1$.

2.4 Avoiding properties

Inclusion/Exclusion appears most frequently in combinatorics not as a means to count $|A_1 \cup \dots \cup A_n|$ directly but rather as a means to count everything not in $A_1 \cup \dots \cup A_n$.

For example, let $[m] = {1,,m} and suppose we want to count the number of functions $f : [m] \to [n]$ which don’t miss anything in the codomain. I.e. if $A_i$ is the set of functions where $f(x)$ never equals $i$, then we want to count every function not in any set $A_i$.

Let $X$ be the total set of functions. Then to count the functions avoiding $A_1 \cup \dots \cup A_n$ we do

\[\begin{align*} |X \setminus (A_1 \cup \dots A_n)| &= |X| - |A_1 \cup \dots A_n| \\ &= |X| - \sum_i |A_i| + \sum_{i < j} |A_i \cap A_j| - \cdots \end{align*}\]

Caution

The formula $|A \setminus B| = |A| - |B|$ works only when $B$ is contained entirely inside $A$.

2.5 Simplifying notation.

Let $\mathscr{P} = \{P_1, \dots, P_n\}$ be a collection of sets representing negative properties—conditions we want to avoid. For a subset $S \subseteq \{1,\dots,n\}$, let $N_\ge(S)$ be the number of items satisfying at least those properties in $S$. I.e. $\bigcap_{i \in S} P_i$. We will say “$x$ satisfies $S$” for short. Also, if $S = \{a,b,c\}$, let us write for example, $N_\ge(a,b,c)$ instead of $N_\ge(\{a,b,c\})$ for simplicity.

Let $N_{=}(S)$ be the number of $x$ satisfying exactly those properties in $S$ and no properties not in $S$. When $\mathscr{P}$ represents properties we wish to avoid, then $N_{=}(\varnothing)$ is the number of elements satisfying none of the properties.

Theorem 2.1 (Inclusion/Exclusion) \[\begin{align*} N_{=}(\varnothing) &= N_{\ge}(\varnothing) - \sum_i N_\ge(i) + \sum_{i < j} N_\ge(i,j) - \cdots \\ &= \sum_{S} (-1)^{|S|} N_\ge(S). \end{align*}\]

Proof. As in Section 2.3, we will break up the sum focusing on each element. So first, we will write \[ \sum_{S} (-1)^{|S|} N_\ge(S) = \sum_S (-1)^{|S|} \sum_{\substack{x \\ x \text{ satisfies } S}} 1 \]

Here we replace the number $N_\ge(S)$ by a count of $1$ for each element $x$ which satisfies $S$. This introduces a second sum into the picture and that will allow us to swap the order of summations. Currently, the second sum is over all $x$ with respect to the relation “$x$ satisfies $S$.” When we put the sum over $x$ outside, we still have the relation “$x$ satisfies $S$” but rather than summing over all $x$ with this property, we sum over all $S$:

\[ \sum_S (-1)^{|S|} \sum_{\substack{x \\ x \text{ satisfies } S}} 1 = \sum_x \sum_{\substack{S \\ x \text{ satisfies } S}} (-1)^{|S|}. \]

We also move the $(-1)^|S|$ inside the second sum because that quantity depends on $|S|$.

Next, just as we did in Section 2.3, let us say that $x$ satisfies exactly $P_{i_1}, \dots, P_{i_m}$ ($m$ will depend on $x$) and let $S_x = \{i_1, \dots, i_m\}$. This set is the largest set that $x$ satisfies. Every other set that $x$ satisfies will be a subset of $S_x$.

We now break up our sum based on the size of those subsets $S \subseteq S_x$, using the binomial coefficients to count the number of such $S$:

\[ \sum_x \sum_{\substack{S \\ x \text{ satisfies } S}} (-1)^{|S|} = \sum_x \sum_{k = 0}^m \underbrace{\binom{m}{k} (-1)^k}_{\substack{|S| = k \text{ and } x \text{ satisfies } S \\ \iff |S| = k \text{ and } S \subseteq S_x}}. \]

This, by the Binomial Theorem, is the same as \[ \sum_x (1 - 1)^m. \] Remember here that $m$ depends on $x$.

As discussed in Note 2.1, $0^m = 0$ if $m \ge 1$ but if $m = 0$ then $0^0 = 1$. Saying $m = 0$ means that $x$ satisfies exactly $0$ properties—which is what we are looking for. So the final simplification looks like \[ \sum_x 0^m = \sum_{\substack{x \\ m = 0}} 1 = N_{=}(\varnothing). \]

2.6 Application 1: Surjections

As in Section 2.4, let $X$ be the set of all functions from $[m]$ to $[n]$ and let $P_i$ be the set of functions where $i$ is never an output: $f(x) \neq i$ for any input $x$.

Lemma 2.1

The number of functions from an $m$ element set to an $n$ element set is $n^m$.
The number of functions from an $m$ element set to an $n$ element set that avoid $k$ outputs is $(n - k)^m$.

Proof.

There are $n$ choices for $f(1)$ and $n$ choices for $f(2)$, etc. So there are $n^m$ choices in total for $f(1), \dots, f(m)$.
If we are avoiding $k$ outputs then there are only $n - k$ choices for each of $f(1),\dots,f(m)$ so $(n - k)^m$.

With this in mind, we have $N_\ge(S) = (n - k)^m$ if $|S| = k$ (we avoid at least the specified $k$ outputs). So by inclusion exclusion, the number of functions which avoid no outputs (i.e. surjections) is

\[\begin{align*} &N_\ge(\varnothing) - \sum_i N_\ge(i) + \sum_{i < j} N_\ge(i,j) - \cdots \\ &\hspace{4em} = n^m - \sum_i (n - 1)^m + \sum_{i < j} (n - 2)^m - \cdots. \end{align*}\]

And since there are $\binom{n}{k}$ ways to choose $k$ outputs to avoid, we can also write this as

\[ n^m - \binom{n}1 (n - 1)^m + \binom{n}2 (n - 2)^m - \dots = \sum_{k} \binom{n}k (-1)^k (n - k)^m. \]

The textbook calls this number $S(m,n)$.

Note

In the above application, $N_\ge(S) = (n - k)^m$ only depended on the size $k$ of $S$. This is true in many but not all examples.

2.7 Application 2: Derangements

Let $X$ be the set of all permutations of $[n]$. We wish to count the permutations with no fixed points. So let $P_i$ be the property that $i$ is a fixed point. Then $N_{=}(\varnothing)$ is the number of permutations with zero fixed points. This number is called $d_n$ in the textbook.

Lemma 2.2

The number of permutations of $[n]$ is $n!$
The number of permutations with at least $k$ specified fixed points is $(n - k)!$

Proof.

Discussed in Chapter 2 of the book.
To say that there are $k$ specified fixed points means were are permuting the other $n - k$ items. Similar to (a), there are $(n - k)!$ ways to permute $n - k$ items.

Applying Inclusion/Exclusion, we thus have \[ d_n = n! - \binom{n}1 (n - 1)! + \binom{n}2 (n - 2)! - \dots = \sum_{k} \binom{n}k (-1)^k (n - k)!. \] Again, there are $\binom{n}k$ ways to choose a set $S$ of $k$ fixed points and each of these has the same number $N_\ge(S) = (n - k)!$.