9 Exercises
- Convert \(2, 12, 3, 5, 4, 9, 8, 7, 6, 10, 1, 11\) to a product of cycles and draw the associated digraph.
Hint
Reference: Section 5.1
- start with 1
- there is a 2 in position 1
- there is a 12 in position 2
- keep going…x in position 12…until you get back to 1
- write down the first cycle \((1, 2, 12, \dots)\) (don’t repeat the \(1\) at the end)
- do the same procedure with the next number which hasn’t been seen so far (i.e. 3)
- keep going until every number is part of a cycle
- optionally, throw away cycles of length 1
- Convert \((1,8,12)(2,3,6,7,9)(4,10,11)\) to a shuffle of \(1,\dots,12\)
Hint
Reference: Section 5.1.2
Since the cycles are disjoint (don’t share any numbers), the procedure here is:
- look for each number from 1 to 12
- write down the number following it in its cycle (e.g. 1 is followed by 8 so we write an 8 in the first position of the shuffle, 2 is followed by 3, 3 by 6, etc.)
- if a number does not appear (i.e. 5), then the permutation leaves it unchanged and it remains in its starting position (so you should have a 5 in position 5 at the end)
Show that \((12)(23)(34)(23)(12) = (14)\) by drawing the braid diagram.
Compute the sign of the permutations in 1. and 2.
Hint
Reference: Section 7.5
Regardless of whether the cycles are disjoint or not (here they are), odd cycles are even and even cycles are odd (in terms of number of swaps). So multiply \(1\) for each odd length cycle and \(-1\) for each even length cycle. For example, \((1, 8, 2)\) has an odd length (even number of swaps) so we multiply \(+1\) for it.
- Write \((182635)\) as a product of transpositions.
Hint
Reference: Theorem 5.1
The rule is like \((a,b,c,d) = (a, b)(b, c)(c, d)\). The transpositions are adjacent pairs.
Additional practice
Solutions
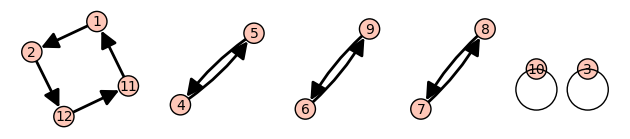
(1, 2, 12, 11)(4, 5)(6, 9)(7, 8)
8, 3, 6, 10, 5, 7, 9, 12, 2, 11, 4, 1
- both even (+1)
(1, 8)(8, 2)(2, 6)(6, 3)(3, 5)